Eulers metode
Contents
Eulers metode#
Eulers metode er en algoritme for å finne numeriske løsninger til ordinære differensialligninger. I naturvitenskapen beskriver slike likninger som oftest en størrelse og endringen av denne størrelsen over tid. Eksempler på dette kan være populasjonsvekst i en bakteriekultur eller fartsendring til et objekt som faller i et gravitsjonsfelt. Eulers metode brukes for å finne numeriske løsninger på slike problemer når du kjenner en initialverdi.
Som et generelt utgangspunkt for Eulers metode antar vi at vi har en ordinær differensiallikning på formen:
I dette eksemplet tenker vi oss at vi har en funksjon \(y\) (som vi ikke vet hvordan ser ut) og differensiallikningen \( y' = y \) (som beskriver hvordan systemet endrer seg). Vi har i tillegg initialbetingelsen \( y(0) = 1 \). Dette kan for eksempel være en beskrivelse av eksponentiell vekst i en bakteriekultur, hvor vi vet antall bakterier vi starter med ved tidspunktet \( t = 0 \).
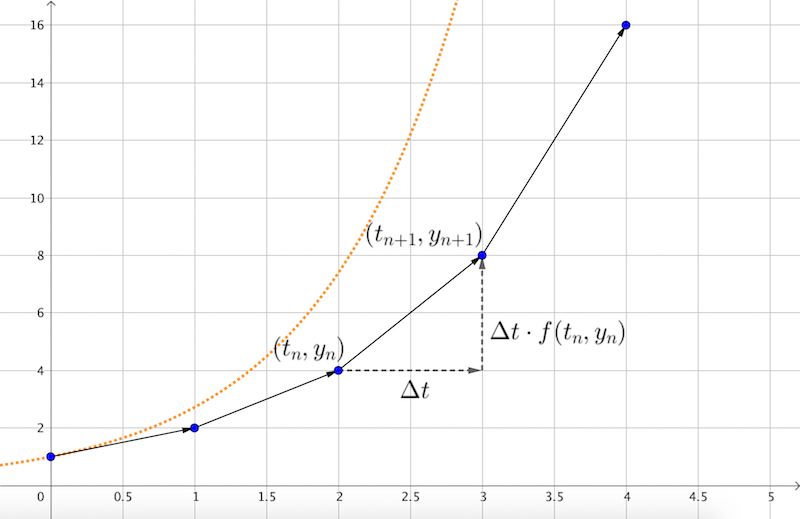
Vi ønsker nå å bruke Eulers metode for å finne denne verdien numerisk. For å få til dette må vi starte et sted som vi vet noe om. I dette tilfellet bruker vi initialbetingelsen \( y(0) = 1 \), og starter derifra. Vi må også bestemme oss for en \( \Delta t \) som er hvor store “skritt” vi skal ta mellom hver beregning.
Vi tar utgangspunkt i \( y' = y \), og skriver \(y'\) som \(\Delta y / \Delta t\):
Her er \(\Delta y\) forskjellen mellom nåværende og neste y-verdi, når vi har beveget oss med tidsskrittet \(\Delta t\). Vi kan skrive det som:
Vi gjør om slik at vi får et uttrykk for neste y-verdi:
Vi skal nå regne ut \(y'(0)\) med utgangspunkt i initialbetingelsen. Vi vet at \(y'= y\) og \(y(0) = 1\). Dette betyr at \(y'(0)=1\).
Neste skritt er å øke \(t\) med \(\Delta t\) og regne ut en gang til. Vi lar \(\Delta t = 1\)
Vi kan nå bruke dette resultatet til å regne ut neste verdi: $\(y(2) = y(1) + \Delta t \cdot y(1) = 2 + 1 \cdot 2 = 4\)$
Slik kan vi fortsette helt til vi har regnet ut \(y(5)\) som i tabellen under.
\(t\) |
\(y\) |
\(y'\) |
|---|---|---|
0 |
1 |
1 |
1 |
2 |
2 |
2 |
4 |
4 |
3 |
8 |
8 |
4 |
16 |
16 |
5 |
32 |
32 |
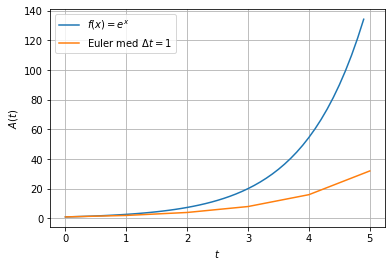
I dette eksemplet har vi ikke sagt noe om hvordan funksjonen \(y\) ser ut, og normalt kjenner vi heller ikke denne. I dette tilfellet vet vi det, og vi har at \(y\) er eksponentialfunksjon \(e^x\). Siden vi her kjenner den virkelige funksjonen, kan vi sammenlikne våre numeriske tilnærminger med de virkelige verdiene. Vi kjenner også startverdien \(y_0\).
# Importerer nødvendige biblioteker
import matplotlib.pyplot as plt
import numpy as np
# Initialbetingelser
y0 = 1
delta_t = 1
# For hvilken t skal beregningene stoppe?
max_t = 5
# Eksakt løsning
def A(x, k):
return k * np.exp(x)
# Eulers metode for denne spesifikke problemstillingen
def next_y(t, yn):
return yn + t * yn
# x-verdier for plotting av eksakt løsning
x = np.arange(0, max_t, 0.1)
y = []
# Regner ut eksakt løsning
for i in x:
y.append(A(i, y0))
# x-verdier for plotting av Euler
xe = np.arange(0, max_t, delta_t).tolist()
# Initialiserer med startverdien for ye
ye = [y0]
# Bruker Eulers metode for å regne ut neste y-verdi
for verdi in xe:
ye.append(next_y(delta_t, ye[-1]))
# Legger til den siste x-verdien
xe.append(xe[-1] + delta_t)
# Utskrift av data
plt.grid() # Lager rutenett
plt.xlabel('$t$') # Merker x-aksen
plt.ylabel('$A(t)$') # Merker y-aksen
plt.plot(x, y, label='$f(x)=e^x$')
plt.plot(xe, ye, label='Euler med $\Delta t={}$'.format(delta_t))
plt.legend()
plt.show()
Oppsummering#
Gitt at vi har en førsteordens lineær differensiallikning:
Vi har også gitt initialbetingelsene:
Vi bestemmer oss for en “skrittlengde” \(\Delta x\) som er avstanden mellom hvert nye estimat vi beregner med Eulers metode. En liten \(\Delta x\) gir mer presise estimater, men “koster mer” i form av mange beregninger som må utføres. Med Eulers metode kan vi nå finne estimater for neste x og y:
Oppgaver#
Ta utgangspunkt i eksempelet over. Endre på step-verdien \(\Delta x\), gjør den gradvis mindre og mindre (la den nærme seg 0). Hva observerer du?
Kan du løse differensiallikningen \(\frac{dy}{dx}=x+2y\) numerisk når \(y(0)=0\)? Bruk \(\Delta x = 0.1\). Finn eksakt løsning med f.eks Wolfram Alpha, og sammenlign med funksjonen du kommer frem til.
En realistisk modell for luftmotstand kan være \(L = k \cdot v^2\). Lag et program som beregner \(v(t)\) ved hjelp av Eulers metode når du vet at \( \sum F = G - L \). (Hint: Husk at \(F = m \cdot a = m \cdot v'\))
Lag et program som viser hvordan en bakteriekultur vokser når vi starter med \(20 \) bakterier ved tiden \(t=0\) s. Populasjonen dobles hver time. Hva er populasjonen etter 7 timer, og når vil populasjonen nå \(1 \cdot 10^6\) bakterier.
Lag et program som bruker Eulers metode på en annen modell som du velger selv.

